1184.公交站间的距离
题目描述
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
1
2
3
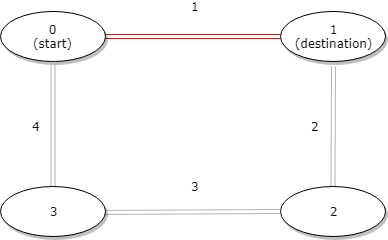
| 输入:distance = [1,2,3,4], start = 0, destination = 1
输出:1
解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
|
示例 2:
1
2
3
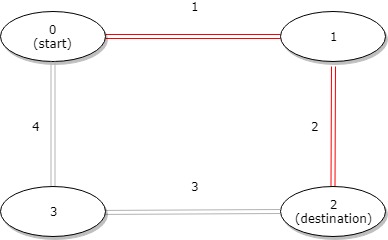
| 输入:distance = [1,2,3,4], start = 0, destination = 2
输出:3
解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
|
示例 3:
1
2
3
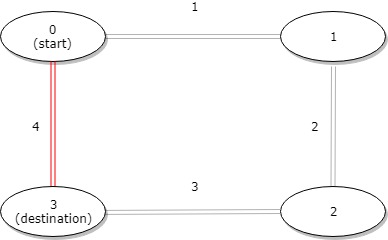
| 输入:distance = [1,2,3,4], start = 0, destination = 3
输出:4
解释:公交站 0 和 3 之间的距离是 6 或 4,最小值是 4。
|
提示:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
解法1:暴力模拟
思路:题中已经说了,只有两种走法要么逆时针,要么顺时针,将两种走法都走一遍,选一个距离最小的即为结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
int n=distance.size();
int l=start,r=destination;
int suml=0,sumr=0;
while(l!=r)
{
suml+=distance[l];
if(l==n-1)
l=0;
else l++;
}
l=start,r=destination;
while(l!=r)
{
sumr+=distance[r];
if(r==n-1)
r=0;
else
r++;
}
return min(suml,sumr);
}
};
|
1185.一周中的第几天
题目描述
给你一个日期,请你设计一个算法来判断它是对应一周中的哪一天。
输入为三个整数:day、month 和 year,分别表示日、月、年。
您返回的结果必须是这几个值中的一个 {"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"}。
示例 1:
1
2
| 输入:day = 31, month = 8, year = 2019
输出:"Saturday"
|
示例 2:
1
2
| 输入:day = 18, month = 7, year = 1999
输出:"Sunday"
|
示例 3:
1
2
| 输入:day = 15, month = 8, year = 1993
输出:"Sunday"
|
提示:
- 给出的日期一定是在
1971 到 2100 年之间的有效日期。
解法1:暴力模拟
我们知道公元1年1月1日是星期一,那么我们只要求出当前日期与公元1年1月1日的差,再对7取余,便可算到当前是星期几
先算出中间有多少个闰年,因为闰年比平年多1天,
然后算出当前年已经过去的月份的天数,再加上这个月的已经过的天数-1,再加上过去年份的天数已经闰年数
注意:若当前年为闰年要减去1天,因为当前年并没有过完,但算闰年的时候已经算上了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
string dayOfTheWeek(int day, int month, int year) {
int ya=year/4;
int a[12]={31,28,31,30,31,30,31,31,30,31,30,31};
int ms=0;
for(int i=0;i<month-1;i++)
ms+=a[i];
if(year%4==0&&month>2)
ms+=1;
int ys=(year-1)*365+ya+ms+day-1;
if(year%4==0)
ys-=1;
string m[7]={"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
return m[ys%7];
}
};
|
1186.删除一次得到子数组的最大和
题目描述
给你一个整数数组,返回它的某个 非空 子数组(连续元素)在执行一次可选的删除操作后,所能得到的最大元素总和。
换句话说,你可以从原数组中选出一个子数组,并可以决定要不要从中删除一个元素(只能删一次哦),(删除后)子数组中至少应当有一个元素,然后该子数组(剩下)的元素总和是所有子数组之中最大的。
注意,删除一个元素后,子数组 不能为空。
请看示例:
示例 1:
1
2
3
| 输入:arr = [1,-2,0,3]
输出:4
解释:我们可以选出 [1, -2, 0, 3],然后删掉 -2,这样得到 [1, 0, 3],和最大。
|
示例 2:
1
2
3
| 输入:arr = [1,-2,-2,3]
输出:3
解释:我们直接选出 [3],这就是最大和。
|
示例 3:
1
2
3
4
| 输入:arr = [-1,-1,-1,-1]
输出:-1
解释:最后得到的子数组不能为空,所以我们不能选择 [-1] 并从中删去 -1 来得到 0。
我们应该直接选择 [-1],或者选择 [-1, -1] 再从中删去一个 -1。
|
提示:
1 <= arr.length <= 10^5-10^4 <= arr[i] <= 10^4
解法1:动态规划
1.建立一个dp二维数组dp[n][2];
dp[i][0]表示 不 删除元素从0到当前i位置的最大子数组和
dp[i][1]表示删除1个元素从0到当前i位置的最大子数组和
2.写出状态转移方程
不删除元素状态转移方程很自然写出来,leetcode53与这一步相同
dp[i][0]=max(dp[i-1][0]+arr[i],arr[i])
删除1个元素状态转移方程
dp[i][1]=max(dp[i-1][0],dp[i-1][1]+arr[i])
意思就是 最大值要么是前面已经删除了1个元素+当前元素 要么是前面没有删除元素,删除当前元素
3.每次循环判断最大值res,循环遍历完毕返回res得到结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
int maximumSum(vector<int>& arr) {
int n=arr.size();
vector<vector<int>> dp(n,vector<int>(2,0));
dp[0][0]=arr[0];
dp[0][1]=0;
int res=arr[0];
for(int i=1;i<n;i++)
{
dp[i][0]=max(dp[i-1][0]+arr[i],arr[i]);
dp[i][1]=max(dp[i-1][1]+arr[i],dp[i-1][0]);
res=max(dp[i][0],res);
res=max(dp[i][1],res);
}
return res;
}
};
|
1187.使数组严格递增
题目描述
给你两个整数数组 arr1 和 arr2,返回使 arr1 严格递增所需要的最小「操作」数(可能为 0)。
每一步「操作」中,你可以分别从 arr1 和 arr2 中各选出一个索引,分别为 i 和 j,0 <= i < arr1.length 和 0 <= j < arr2.length,然后进行赋值运算 arr1[i] = arr2[j]。
如果无法让 arr1 严格递增,请返回 -1。
示例 1:
1
2
3
| 输入:arr1 = [1,5,3,6,7], arr2 = [1,3,2,4]
输出:1
解释:用 2 来替换 5,之后 arr1 = [1, 2, 3, 6, 7]。
|
示例 2:
1
2
3
| 输入:arr1 = [1,5,3,6,7], arr2 = [4,3,1]
输出:2
解释:用 3 来替换 5,然后用 4 来替换 3,得到 arr1 = [1, 3, 4, 6, 7]。
|
示例 3:
1
2
3
| 输入:arr1 = [1,5,3,6,7], arr2 = [1,6,3,3]
输出:-1
解释:无法使 arr1 严格递增。
|
提示:
1 <= arr1.length, arr2.length <= 20000 <= arr1[i], arr2[i] <= 10^9
解法1:动态规划+二分
定义dp[i],表示0~i保存i元素存在的最小 操作 数。
dp[i]=min(dp[i],dp[j]+(i-j-1)) 其中j从0到i-1,arr1[j]<arr1[i],(i-j-1)为替换的元素个数。被替换元素的下标从j+1到i-1,所需要的替换元素arr2[k]满足arr1[j]<arr2[k]<arr1[i]
1.对arr2进行预处理,先排序,然后去掉重复元素。这样我们就可以通过二分查找找到替换元素所在的位置
2.算出dp[i]我们发现,我们并没有判断最后一个arr1的最后一个数字是否替换,同时状态转移方程也不能满足arr1的第一个元素,无法判断第一个元素是否替换。
我们可以做以下处理,(1)在arr1的末位添加一位数字INT_MAX,这个数字不需要被考虑替换,我们也就可以判断arr1原数组最后一个数字是否替换。(2)在arr1的首部添加一个比任何值小的数,这样我们也就能判断arr1原数组的第一个元素是否替换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| class Solution {
public:
int makeArrayIncreasing(vector<int>& arr1, vector<int>& arr2) {
int n=arr1.size();
vector<int> a1(n+2,0);
a1[0]=-1;
for(int i=0;i<n;i++)
{
a1[i+1]=arr1[i];
}
a1[n+1]=INT_MAX;
vector<int> dp(n+2,0);
sort(arr2.begin(),arr2.end());
vector<int>::iterator ite=unique(arr2.begin(),arr2.end());
arr2.erase(ite,arr2.end());
for(int i=1;i<=n+1;i++)
{
dp[i]=INT_MAX;
for(int j=0;j<i;j++)
{
if(a1[i]<=a1[j]||dp[j]==INT_MAX)
continue;
if(find(j,i,a1,arr2))
{
dp[i]=min(dp[i],dp[j]+(i-j-1));
}
}
}
return dp[n+1]==INT_MAX?-1:dp[n+1];
}
bool find(int j,int i,vector<int>& a1,vector<int>& arr2)
{
if(j+1==i)
return true;
int minIdx=bs1(a1[j],arr2);
int maxIdx=bs2(a1[i],arr2);
if(minIdx==arr2.size()||maxIdx==-1)
return false;
return (i-j-1)<=(maxIdx-minIdx+1);
}
int bs1(int target,vector<int>& arr2)
{
int l=0,r=arr2.size()-1;
while(l<r)
{
int mid=l+(r-l)/2;
if(arr2[mid]<=target)
l=mid+1;
else
r=mid;
}
return arr2[l]>target?l:arr2.size();
}
int bs2(int target,vector<int>& arr2)
{
int l=0,r=arr2.size()-1;
while(l<r)
{
int mid=l+(r-l+1)/2;
if(arr2[mid]>=target)
r=mid-1;
else
l=mid;
}
return arr2[l]<target?l:-1;
}
};
|
时间复杂度:O($N^2LogM$)
解法2:再次优化
将二分查找部分再次优化,在第一层循环内直接找到小于元素a[i]的最大下标r,然后我们找到允许替换的最大下标(即若能替换这部分,若是比这个下标还大,arr2部分数组的长度就比i-j-1小了),也就是直接找到
l=r-(i-j-1)+1,判断arr2[l]跟a[j]的关系,若arr2[l]大于a[j]表示可以替换这部分,否则就是不能替换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class Solution {
public:
int makeArrayIncreasing(vector<int>& arr1, vector<int>& arr2) {
int n=arr1.size();
vector<int> a1(n+2,0);
a1[0]=-1;
for(int i=0;i<n;i++)
{
a1[i+1]=arr1[i];
}
a1[n+1]=INT_MAX;
vector<int> dp(n+2,0);
sort(arr2.begin(),arr2.end());
vector<int>::iterator ite=unique(arr2.begin(),arr2.end());
arr2.erase(ite,arr2.end());
for(int i=1;i<=n+1;i++)
{
dp[i]=INT_MAX;
int r=bs2(a1[i],arr2);
for(int j=0;j<i;j++)
{
if(a1[i]<=a1[j]||dp[j]==INT_MAX)
continue;
int l=r-(i-j-1)+1;
if(j+1==i||r>=0&&l>=0&&arr2[l]>a1[j])
{
dp[i]=min(dp[i],dp[j]+(i-j-1));
}
}
}
return dp[n+1]==INT_MAX?-1:dp[n+1];
}
int bs2(int target,vector<int>& arr2)
{
int l=0,r=arr2.size()-1;
while(l<r)
{
int mid=l+(r-l+1)/2;
if(arr2[mid]>=target)
r=mid-1;
else
l=mid;
}
return arr2[l]<target?l:-1;
}
};
|
时间复杂度:O($n^2$)


