基础学习|主动学习综述
主动学习通过一定的算法查询最有用的未标记样本,并交由专家进行标记,然后用查询到的样本训练分类模型来提高模型的精确度。
不同于被动学习被动的接受知识,主动学习能够选择性地获取知识。
如何从中挑选出对训练贡献度高的样例,标注后补充到训练集中来提升分类器性能是主动学习研究方向之一。
1.什么是主动学习AL
为了尽可能地减小训练集及标注成本,在机器学习领域中,提出主动学习(active learning)方法,优化分类模型。
主动学习(active learning),指的是这样一种学习方法:有的时候,有类标的数据比较稀少而没有类标的数据是相当丰富的,但是对数据进行人工标注又非常昂贵,这时候,学习算法可以主动地提出一些标注请求,将一些经过筛选的数据提交给专家进行标注。
这个筛选过程就是主动学习主要研究的地方.
主要目标:是在保证分类精度不降低的前提下有效地发现训练数据集中高信息量的样本,使训练的分类器在较低的标注下高效地训练模型。
主动学习是机器学习(更普遍的说是人工智能)的一个子领域,在统计学领域也叫查询学习、最优实验设计。“学习模块”和“选择策略”是主动学习算法的2个基本且重要的模块。主动学习通过“选择策略”主动从未标注的样本集中挑选部分(1个或N个)样本让相关领域的专家进行标注;然后将标注过的样本增加到训练数据集给“学习模块”进行训练;当“学习模块”满足终止条件时即可结束程序,否则不断重复上述步骤获得更多的标注样本进行训练。
1.1基本思想
主动学习的模型如下:
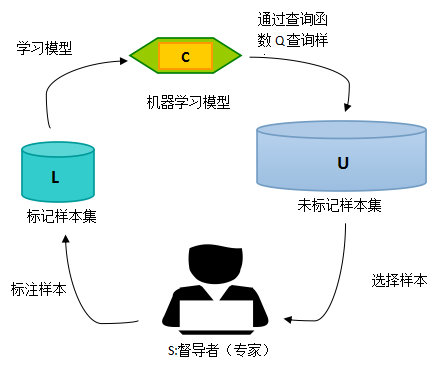
A=(C,Q,S,L,U)
其中 C 为一组或者一个分类器,L是用于训练已标注的样本。Q 是查询函数,用于从未标注样本池U中查询信息量大的信息,S是督导者,可以为U中样本标注正确的标签。学习者通过少量初始标记样本L开始学习,通过一定的查询函数Q选择出一个或一批最有用的样本,并向督导者询问标签,然后利用获得的新知识来训练分类器和进行下一轮查询。主动学习是一个循环的过程,直至达到某一停止准则为止。
刚才说到查询函数Q用于查询一个或一批最有用的样本。那么,什么样的样本是有用的呢?即查询函数查询的是什么样的样本呢?在各种主动学习方法中,查询函数的设计最常用的策略是:不确定性准则(uncertainty)和差异性准则(diversity)。
对于不确定性,我们可以借助信息熵的概念来进行理解。信息熵是衡量信息量的概念,也是衡量不确定性的概念。信息熵越大,就代表不确定性越大,包含的信息量也就越丰富。事实上,有些基于不确定性的主动学习查询函数就是使用了信息熵来设计的,比如熵值装袋查询(Entropy query-by-bagging)。所以,不确定性策略就是要想方设法地找出不确定性高的样本,因为这些样本所包含的丰富信息量,对我们训练模型来说就是有用的。
那么差异性怎么来理解呢?之前说到查询函数每次迭代中会查询一个或者一批样本。我们希望所查询的样本提供的信息是全面的,各个样本提供的信息不重复不冗余,即样本之间具有一定的差异性。在每轮迭代抽取单个信息量最大的样本加入训练集的情况下,每一轮迭代中模型都被重新训练,以新获得的知识去参与对样本不确定性的评估可以有效地避免数据冗余。但是如果每次迭代查询一批样本,那么就应该想办法来保证样本的差异性,避免数据冗余。
1.2与半监督学习不同
半监督学习和直推学习(transductive learning)以及主动学习,都属于利用未标记数据的学习技术,但基本思想还是有区别的。
主动学习的“主动”,指的是主动提出标注请求,也就是说,还是需要一个外在的能够对其请求进行标注的实体(通常就是相关领域人员),即主动学习是交互进行的。
而半监督学习,特指的是学习算法不需要人工的干预,基于自身对未标记数据加以利用。
(1)半监督学习一般不需要人工参与,是通过具有一定分类精度的基准分类器实现对未标注样例的自动标注;而主动学习需要将挑选出的高价值样例进行人工准确标注。
(2)半监督学习通过用计算机进行自动或半自动标注代替人工标注,虽然有效降低了标注代价,但其标注结果依赖于用部分已经标注样例训练出的基准分类器的分类精度,因此并不能保证标注结果完全正确。
2查询策略
查询策略(Query Strategy Frameworks)是主动学习的核心之处,通常可以选择以下几种查询策略:
- 不确定性采样的查询(Uncertainty Sampling);
- 基于委员会的查询(Query-By-Committee);
- 基于模型变化期望的查询(Expected Model Change);
- 基于误差减少的查询(Expected Error Reduction);
- 基于方差减少的查询(Variance Reduction);
- 基于密度权重的查询(Density-Weighted Methods)。
2.1 不确定性采样(Uncertainty Sampling)
这类方法选择那些当前基准分类器最不能确定其分类的样例进行标注。这类方法以信息熵作为衡量样例所含信息量大小的度量,而信息熵最大的样例正是当前分类器最不能确定其分类的样例。从几何角度看,这种方法优先选择靠近分类边界的样例。
顾名思义,不确定性采样的查询方法就是将模型中难以区分的样本数据提取出来,提供给业务专家或者标注人员进行标注,从而达到以较快速度提升算法效果的能力。而不确定性采样方法的关键就是如何描述样本或者数据的不确定性,通常有以下几种思路:
- 置信度最低(Least Confident);
- 边缘采样(Margin Sampling);
- 熵方法(Entropy);
2.1.1 Least Confident
对于二分类或者多分类的模型,通常它们都能够对每一个数据进行打分,判断它究竟更像哪一类。例如,在二分类的场景下,有两个数据分别被某一个分类器预测,其对两个类别的预测概率分别是:(0.9,0.1) 和 (0.51, 0.49)。在此情况下,第一个数据被判定为第一类的概率是 0.9,第二个数据被判定为第一类的概率是 0.51,于是第二个数据明显更“难”被区分,因此更有被继续标注的价值。
2.1.2 Margin Sampling
边缘采样(margin sampling)指的是选择那些极容易被判定成两类的样本数据,或者说这些数据被判定成两类的概率相差不大。边缘采样就是选择模型预测最大和第二大的概率差值最小的样本。
特别地,如果针对二分类问题,least confident 和 margin sampling 其实是等价的。
2.1.3 Entropy
在数学中,可以使用熵(Entropy)来衡量一个系统的不确定性,熵越大表示系统的不确定性越大,熵越小表示系统的不确定性越小。因此,在二分类或者多分类的场景下,可以选择那些熵比较大的样本数据作为待定标注数据。
相较于 least confident 和 margin sample 而言,entropy 的方法考虑了该模型对某个 的所有类别判定结果。而 least confident 只考虑了最大的概率,margin sample 考虑了最大的和次大的两个概率。
2.2 基于委员会的查询(Query-By-Committee)
这类方法选择那些训练后能够最大程度缩减版本空间的样例进行标注。在二值分类问题中,这类方法选择的样例总是差不多平分版本空间。
QBC算法从版本空间中随机选择若干假设构成一个委员会,然后选择委员会中的假设预测分歧最大的样例进行标注。为了优化委员会的构成,可以采用Bagging,AdaBoost等分类器集成算法从版本空间中产生委员会。
除了考虑单个模型的不确定性采样方法之外,还可以考虑多个模型的场景,这就是类似集成学习的方法。通过多个模型投票的模式,来选择出那些较“难”区分的样本数据。在 QBC(Query-By-Committee)的技术方案中,可以假设有 个模型,其参数分别是
,并且这些模型都是通过数据集
的训练得到的。
如果不需要考虑每个模型的检测效果,其实可以考虑类似不确定性采样中的 least confident 和 margin sampling 方法。可以选择某一个分类器难以区分的样本数据,也可以选择其中两三个分类器难以区分的数据。但是如果要考虑所有模型的分类效果的时候,则还是需要熵(Entropy)或者 KL 散度等指标。因此,QBC 通常也包括两种方法:
- 投票熵(Vote Entropy):选择这些模型都无法区分的样本数据;
- 平均 KL 散度(Average Kullback-Leibler Divergence):选择 KL 散度较大的样本数据。
2.3 基于泛化误差缩减的方法
这类方法试图选择那些能够使未来泛化误差最大程度减小的样例。其一般过程为:首先选择一个损失函数用于估计未来错误率,然后将未标注样例集中的每一个样例都分别估计其能给基准分类器带来的误差缩减,选择估计值最大的那个样例进行标注。
这类方法直接针对分类器性能的最终评价指标,但是计算量较大,同时损失函数的精度对性能影响较大。
2.3.1 期望模型变化(Expected Model Change)
模型变化最大其实可以选择那些使得梯度变化最大的样本数据。
2.3.2 期望误差减少(Expected Error Reduction)
可以选择那些通过增加一个样本就使得 loss 函数减少最多的样本数据。
2.3.3 方差减少(Variance Reduction)
选择那些方差减少最多的样本数据。
2.3.4 基于密度权重的选择方法(Density-Weighted Methods)
有的时候,某个数据点可能是异常点或者与大多数数据偏差较大,不太适合做样本选择或者区分,某些时候考虑那些稠密的,难以区分的数据反而价值更大。于是,可以在使用不确定性采样或者 QBC 方法的时候,将样本数据的稠密性考虑进去。
2.4 其它方法
COMB算法:组合三种不同的学习器,迅速切换到当前性能最好的学习器从而使选择样例尽可能高效。
多视图主动学习:用于学习问题为多视图学习的情况,选择那些使不同视图的预测分类不一致的样例进行学习。这种方法对于处理高维的主动学习问题非常有效。
预聚类主动学习:预先运行聚类算法预处理,选择样例时优先选择最靠近分类边界的样例和最能代表聚类的样例(即聚类中心)。
3 深度主动学习DAL
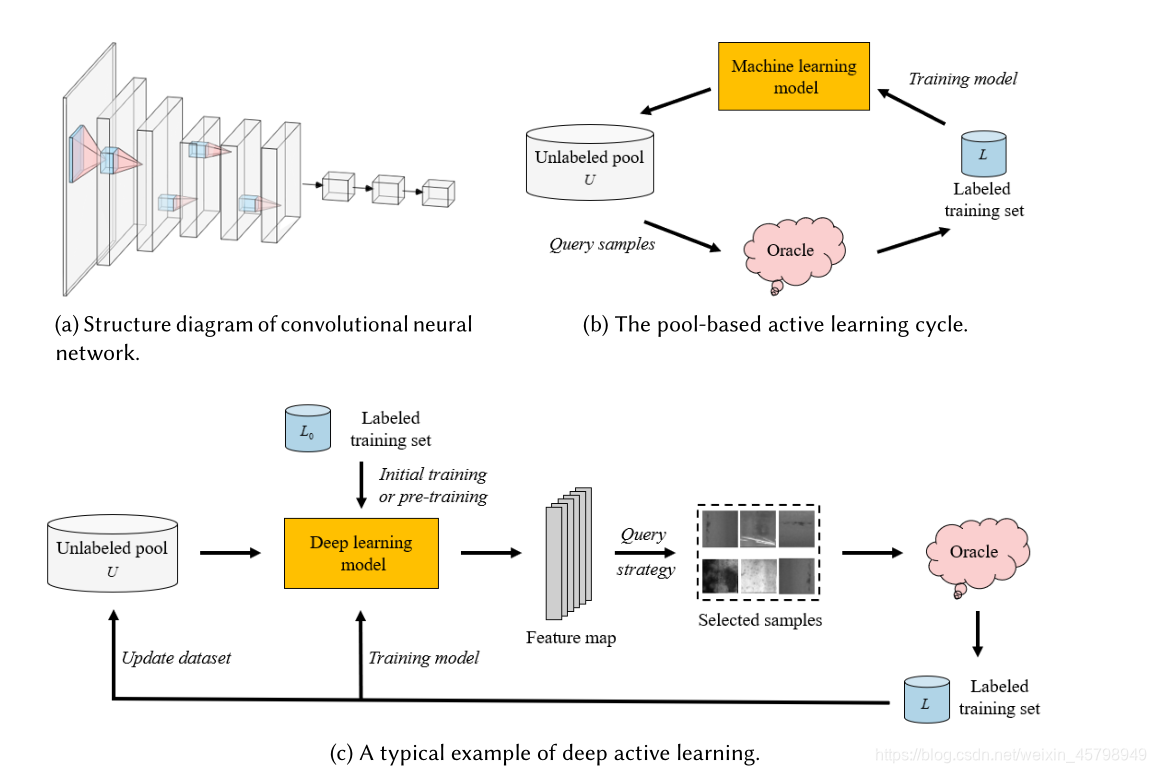
(a)一个常见的深度学习model:卷积神经网络
(b)基于池的主动学习周期:使用查询策略在无标记池U中查询样本交给检测器进行标注,然后将查询的样本添加到标记训练数据集L中继续训练,接着使用新学习的知识进行下一轮查询。重复这个过程,直到标注预算被耗尽或者达到预先设定的终止条件。
(c)深度主动学习的典型例子: 深度学习model的参数θ在初始化标签训练集L0上进行初始化或者预训练,无标记池U的样本通过深度学习model提取特征。然后基于相应的查询策略挑选样本,并在oracle中查询标签,形成新的标签训练集,接着在L上训练深度学习model,同时更新。重复这个过程,直到标注预算被耗尽或者达到预先设定的终止条件。
从图1(c)中的DAL框架示例中,我们可以将DAL框架大致分为两部分:即对未标记数据集的AL查询策略和DL模型训练方法。
3.1 DAL中的查询策略优化
批次模式DAL(BMDAL)
DAL与经典AL的主要区别在于DAL采用的是基于batch的样本查询方式。在传统的AL中大部分算法采用 one by one 的方式进行查询,这导致学习模型被频繁训练,而训练数据却几乎没有变化。这种查询方式得到的训练集在DL模型的训练中不仅低效且极易引起过拟合。因此,BMDAL的研究是必要的。在BMDAL的语境中,在每一个获取步骤,我们依据所使用的获取函数以及在训练过的深度模型对候选的未标记数据样本的batch进行评分, 从而选择一批新的数据样本。
一个天真的想法是基于one-by-one的策略,连续查询一个批次的样本。选择查询获取分数最高的前些样本。显然,这种方法是不可行的,因为这极有可能选择一组信息丰富但却相似的样本。类似的样本为模型提供的信息基本上是相同的,这不仅浪费标注资源,模型也很难真正学到有用的信息。
BMDAL的核心在于查询一组信息丰富且多样的样本。
3.1.1 基于不确定性的混合查询策略
基于不确定性的方法形式简单且较低的计算复杂度,它是AL中是非常受欢迎的一种查询策略。
有很多DAL方法直接采用了这种基于不确定性的采样策略,但是,正如上面所分析的那样这很容易导致批查询样本的多样性不足(没有充分利用数据分布的相关知识),进而导致DL模型训练性能低下甚至失效。一种可行的策略是在一个批查询中采用混合查询策略,以显式或者隐式的方式同时考虑样本的信息量、多样性或者表示形式。
3.1.2 深度贝叶斯主动学习(DBAL)
DBAL将贝叶斯卷积神经网络同AL方法进行结合,使BALD适应了深度学习环境,从而为高维数据开发了一个新的AL框架。它正是采用上述方法首先对CNN权重将进行了高斯先验建模,然后使用变分推断来获得网络预测的后验分布。此外,在实践当中,研究人员往往也使用一种功能强大成本低廉的Monte随机正则化技术来获得后验样本,并在真实数据集上有着很好的表现。并且,这种正则化技术已被证明等价于变分推理。
3.1.3 基于密度的方法应用
基于密度的方法主要是指从集合(核心集)的角度来考察样本的选择。核心集的构建正是这样一种具有代表性的查询策略。这种想法主要受到核心集数据集压缩思想的启发,试图使用核心集来代表整个原始数据集的特征空间的分布,从而降低AL的标注成本。
总的来说,这些查询策略并非相互独立,而是相互联系的。基于Batch的BMDAL为AL查询的样本在DL模型上的更新训练提供了基础。尽管DAL中的查询策略丰富且复杂,但它们大都是为了在BMDAL中兼顾查询批次的多样性与不确定性。而先前基于不确定性的方法往往忽视batch中的多样性,因此,这些方法大致可以被归为两类–它们要么在输入或学习表示空间中设计明确鼓励批次多样性的机制,要么直接测量整个批次的互信息(MI)。
3.2 DAL中的数据不足
AL通常只需要少量的标记样本数据来实现学习和模型更新,而DL则需要大量的标记数据来进行有效的训练。因此,AL和DL的结合要求尽可能多地使用数据策略,而不消耗太多的人力资源来实现DAL模型训练。大多数以前的DAL方法通常只对查询策略所采样的标记样本集进行训练。然而,这忽略了现有未标记数据集的存在,这意味着相应的数据扩展和训练策略没有得到充分利用。这些策略有助于改善DAL训练中标记数据不足的问题,而不增加人工标记成本。因此,对这些策略的研究也是相当有意义的。例如,CEAL通过为模型预测中的高置信度样本分配伪标签,以及通过查询策略采样的标记数据集来丰富训练集。这个扩展的训练集也被用于DL模型的训练。该策略如图4所示。
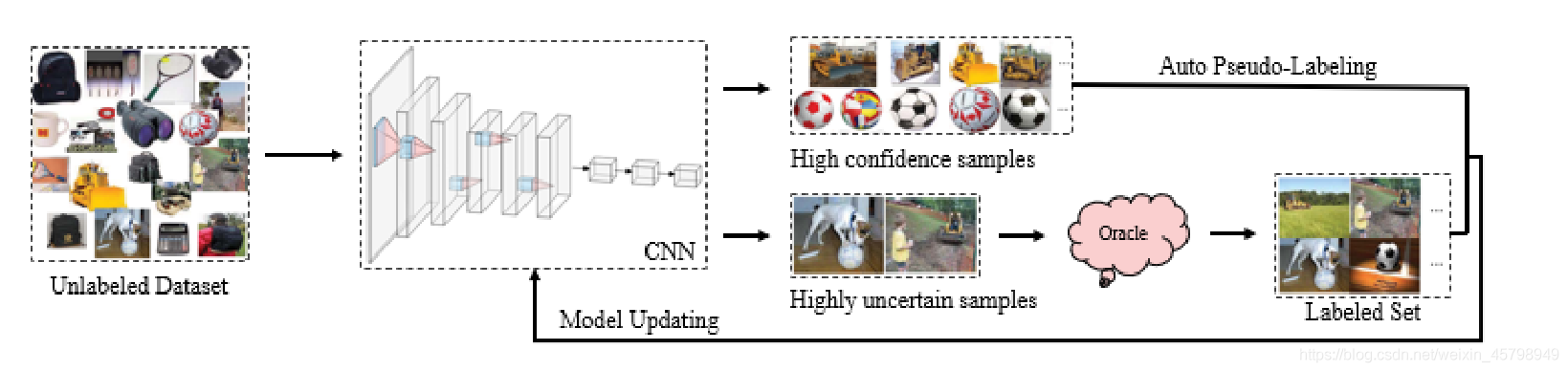
图4.CEAL将未标记数据集中的样本逐步输入初始化的CNN,然后CNN分类器输出两类样本:少量不确定样本和大量具有高预测置信度的样本。通过oracle对少量不确定样本进行标记,并利用CNN分类器对大量高预测置信度样本进行伪标记。然后使用这两种类型的样本对CNN进行微调,并重复更新过程。
另一个非常流行的策略是对有标记和未标记的数据集进行无监督训练,并结合其他策略来训练整个网络结构。
同时,也有研究者考虑使用生成性对抗网络(Generative atteriral Networks,GAN)进行数据扩充。GAAL首次将产生式对抗网络(Generative atrial Network,GAN)引入AL查询方法。GAAL的目标是使用生成性学习来生成比原始数据集更多的信息的样本。
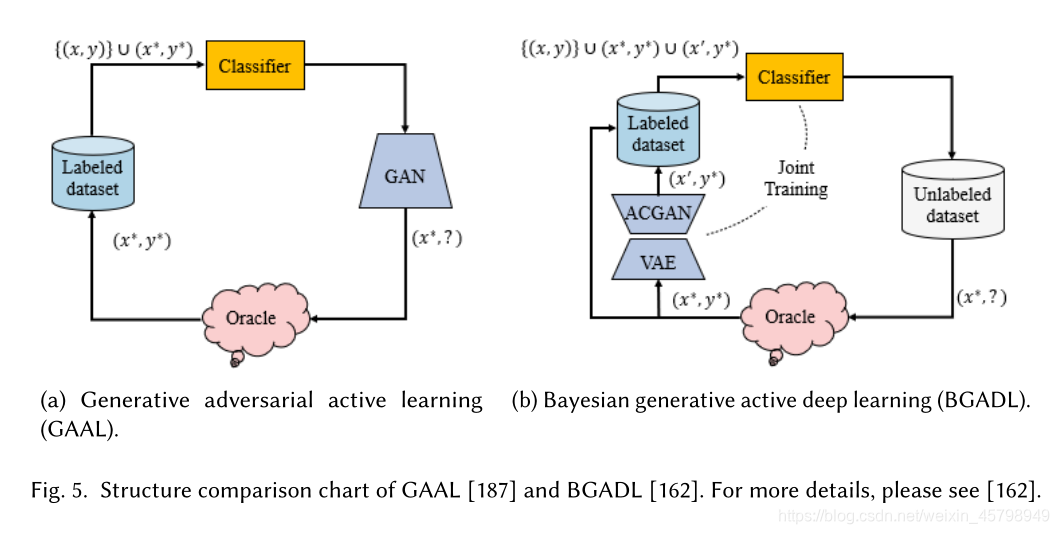
然而,随机数据扩充并不保证生成的样本将比原始数据中包含的信息更多,因此可能会浪费计算资源。因此,BGADL扩展了GAAL的思想,提出了一种贝叶斯生成式主动深度学习方法。更具体地说,BGADL结合了生成性对抗性主动学习(GAAL)、贝叶斯数据扩充、辅助分类器生成对抗网络(ACGAN)和变分自动编码器(V AE)方法,目的是生成属于不同类别的分解区域样本。GAAL和BGADL的结构比较如图5所示。
正如上面说分析的那样,这种在训练方式和数据利用技巧上的探索也是非常有必要的,它在性能上的增益甚至可能超过改变查询策略所代来的性能增益。这实际上是在不增加标注代价的情况下对已有数据信息的充分利用,有助于缓解AL查询样本数量不足以支撑DL模型更新的问题。
3.3 DAL 的各种应用
如今,DAL已经被应用包括但不限于视觉数据处理(例如目标检测,语义分割等),NLP(例如情感分析,问答等),语音和音频处理 ,社交网络分析,医学图像处理,野生动物保护,工业机器人和灾害分析等领域。
如同DL在计算机视觉领域被广泛应用一样,DAL的提出第一个被期待发挥潜力的领域就是计算机视觉。
NLP一直以来都是一个非常具有挑战性的任务。NLP旨在使计算机理解复杂的人类语言,帮助人类处理各种与自然语言相关的任务。数据标签不足也是NLP任务所面临的一个关键性的挑战。
深度主动学习有望在保持性能的情况下,成数量级的减少标注代价。为此,DAL也被广泛的应用于其他领域。
这些应用包括但不限于基因表达、机器人、可穿戴设备数据分析、社交网络和心电信号分析等。
总的来说,DAL目前的应用主要集中在视觉图像处理任务中,对NLP和其他领域也有着相对零散的应用。和DL与AL相比,DAL目前仍然处于研究的初级阶段,相应经典作品还相对较少,但仍然有着和DL一样广阔的应用场景和实用价值。
4 应用
文档分类和信息提取
以贝叶斯方法位基准分类器,使用基于不确定度缩减的样例选择算法进行文本分类。
将EM算法同基于QBC方法的主动学习集合。EM算法能够有效的利用未标注样例中的信息提高基准分类器的分类正确率。而QBC方法能够迅速缩减版本空间。
图像检索
利用SVM作为基准分类器的主动学习算法来处理图像检索。该算法采用最近边界方法作为样例选择算法,同时将图像的颜色、纹理等提取出来作为部分特征进行学习。
入侵检测
由于入侵检测系统较多地依赖专家知识和有效的数据集,所以可以采用主动学习算法降低这种依赖性。
5 总结
在主动学习(Active Learning)领域,其关键在于如何选择出合适的标注候选集给人工进行标注,而选择的方法就是所谓的查询策略(Query Strategy)。查询策略基本上可以基于单个机器学习模型,也可以基于多个机器学习模型,在实际使用的时候可以根据情况来决定。整体来看,主动学习都是为了降低标注成本,迅速提升模型效果而存在的。
参考文献及资料
https://blog.csdn.net/qq_15111861/article/details/85264109
https://blog.csdn.net/qq_38342886/article/details/91356124
https://zhuanlan.zhihu.com/p/239756522
A Survey of Deep Active Learning
https://blog.csdn.net/weixin_45798949/article/details/108842951